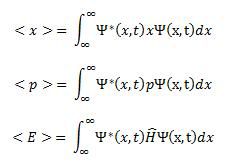3. Numerical Differentiation

3.1 Numerical Differentiation Procedure

Ada 6 jenis Pembezaan Prosedur berangka (Numerical Differentiation Procedure).

1. Differentiation of direct fit polynomial
2. Differentiation of Lagrange polynomial
3. Differentiation of divided different polynomial
4. Differentiation of newton forward-difference polynomial
5. Differentiation of newton-backward-difference polynomial
6. Differentiation based on Taylor series.

2. Interpolasi and Linear Interpolasi

2.1  Interpolasi (Interpolation)

Dari post sebelum ini dalam kategori computational physics, (kesilapan dan ketaktentuan dalam komputer)
kesilapan ke-4 iaitu kesilapan permbundaran akan diatasi dengan cara interpolation (penentudalaman).

Ia adalah cara untuk menghasilkan data yang baru dalam jarak secara diskret yg dikenali sebagai titik data (data point)

Sebagai contoh,

x                    f(x)
0                     0
1                 0.8415
2                 0.9093
3                 0.1411
4               -0.7568
5               -0.9589
6               -0.2794






2.1. Linear Interpolasi (Linear Interpolation)

Seperti contoh dalam untuk menyelesaikan masaalah f(2.5) yang barada di antara 2 dan 3, f(2) = 0.9093, f(3) =  0.1411, yang hasilnya adalah 0.5252.

Biasanya linear interpolasi akan mengambil 2 titik data dan ianya akan memberi formula seperti di bawah..

Contoh,

Diberi f(x) = sin x. andaikan bahawa  X_i  = 2π/4,  X_i+1 = π/2 .. 


Diberi juga f_{i = 0.707 dan} f_{i+1 = 1.000. Maka guna linear interpolasi untuk mendapatkan nilai f(x) di x=3}π/8. Dan apakah nilai kesilapan ∆f(x)?

Jawapan

Kesilapan dan Tidak Ketentuan Dalam Komputer

1) Blunder and bad theory (Kesilapan dan teori salah)
Kesalahan dalam menaip semasa memasukkan kod atau data, maka ia akan menyebabkan  program tidak berjalan dengan sepatutnya.

2) Random error. (kesalahan rawak)
Kesalah ini disebabkan oleh situasi seperti turun naik tenaga elektrik dalam elektronik kerana disebabkan oleh bekalan elektrik, sinar kosmik, atau ada seseorang yang cabut bekalan kuasa..

3) Approximation Error. (Kesilapan penghampiran)
Kesalahan dalam memudahkan jalan kira matematik. Dalam menyelesaikan masaalah matematik, jawapan terakhir adalah hampir tapi tidak tepat dari apa yang sepatutnya seperti cara analisis (matematik biasa).


4) Roundoff error. (kesalahan permbundaran)
Sebagai contoh, dalam operasi pecahan 1/3.. Komputer akan mengeluarkan kepututsan 0.3333... dan ada pembundaran seperti 2/3 = 0.6667. Maka apabila menjalankan operasi matematik seperti 2(1/3)-(2/3), komputer akan menghasilkan,

2(1/3) - 2/3 = 2(0.333) - 0.667
                   = 0.666-0.667
                   = -0.001
Jawapan yg sepatutnya adalah 0.

Introduction to Statistical Physics

Statistical physics.

• is a method to describe the microscopic properties of system based on the average behaviour of its microscopic component.
• uses methods of probability theory and statistics, and particularly the mathematical tools for dealing with large populations and approximations
• Deeper understanding of kinetic theory and thermodynamic properties such as temperature and entropy.
• Its main purpose is to clarify the properties of matter in aggregate.
• More at http://en.wikipedia.org/wiki/Statistical_physics
  
  
• salah satu cara untuk menerangkan sifat mikroskopik sesuatu sistem berdasarkan sifat purata mikrospopik komponennya.
• menggunakan cara teori kebarangkalian dan statistik, dan khususnya matematik untuk populasi yang besar dan berhampiran.
• pemahan secara mendalam untuk teori kinetik dan sifat termodinamik seperti suhu dan entropi.
• Selanjutnya di http://en.wikipedia.org/wiki/Statistical_physics
  
  

Energy states   - The placed when particle are exist in same level but different arrangement.

                       - Tempat di mana zarah akan wujud di tahap yang sama tetapi berbeza kedudukan.

Energy level     - The level which will occupied by particle in different energy.
                       - Tahap yang akan diduduki oleh zarah di dalam tenaga yang berbeza.

Microstate       - Description of the system in microscopic level. Such as position and momentum of particle,
                          or wavefuntion for the quantum system.
                       - Penerangan sesuatu sistem dalam tahap mikroskopik. Contoh seperti kedudukan dan  

                          momentum zarah dan wavafuntion untuk sistem kuantum.

Macrostate      - Description of the macroscopic level such as pressure, temperature, and ect.
                       - Penerangan suatu sistem dalam tahap makroskopik seperti tekanan, suhu, dll.
Degenerate      - More than one energy partition in same level
                       - Lebih dari satu pembahagian tenaga dalam tahap tenaga yang sama.

Nondegenerate- Single energy partition.
                       - Pembahagian tenaga yang tunggal.

Photoelectric Effect (Part 2)

Inspirasi dari "Plank's quantization of electromagnetic radiation", Einstien pada tahun 1905 dengan jayanya memberi penjelasan teori untuk photoelectric emission dalam frekuensi sinaran cahaya. Dia menyatakan cahaya diperbuat dari sel yang mempunyai tenaga tersendiri (hv), yang dipanggil photon. Apabila cahaya yg mempunyai frekuensi f menyinari ke dalam besi, setiap photon akan menghantar segala tenaga hv ke eleketron. Pada masa itu photon dserap oleh electron. Tenaga yang diserap adalah dalam bentuk quanta, hv tanpa mengira keamatan cahaya tersebut. Jika hv lebih besar dari  "metal work function", W, elektron akan ditendang keluar dari besi tersebut. 

Setiap besi mempunyai work funtion yang berbeza, apa yang boleh dilihat seperti gambar di atas,

E=hv

h - plank constant = 6.626068 × 10^-34 m² kg / s

v ataupun f- frekuensi cahaya tersebut

Jika dilihat, potassium mempunyai 2.0eV work funtion, maka tenaga yang kurang dari 2.00 tidak dapat menendang keluar elektron dari potassium.

Einstein telah menulis rumus di bawah untuk menjelaskan secara matematik apa yang berlaku.

                                                           K=hf-W=h(f-f_o)f_o =W/h dan juga dikenali sebagai threshold frequency atau cutoff frequency dalam sesuatu besi.


Apa yang perlu difahami dalam part 2 ini.. Jika frekuensi gelombang cahaya itu lebih rendah dari threshold frequency, maka tiada elektron akan keluar dari besi tersebut. Jika frekuensi  Jika frekuensi gelombang cahaya itu lebih tinggi dari threshold frequency, maka elektron akan ditendang keluar dari besi tersebut.

f  >  f_{o     -Elektron akan ditendang keluar dari besi.}
f < f<sub>o      -Tiada elektron akan ditendang keluar dari besi






Stopping potential, Vs

Stopping potential adalah fenomena apabila elektron yang ditendang keluar akan kembali ke besi sebelum ia sampai ke "electron collector". Maka tenaga yang diperlukan photon untuk ke collector adalah melebihi treshold frequncy dan tenaga yang hilang sewaktu perjalanan elektron tersebut.

maka ia dapat dirumuskan bahawa maksimum tenaga kinetik adalah,</sub>

jika e adalah elektron dan Vo adalah minimum tenaga yang diperlukan untuk menendang elektron keluar, maka

 

dari hubungan kedua2 rumus tersebut,

 

dan,

bentuk graf Vs melawan frekuensi adalah garisan lurus seperti kecerunan h/e. 

Ia menunjukkan stopping potential adalah berkadar langsung denan frekuensi gelombang tersebut.. 

Introduction to Computational Physics

Pengenalan

Sebelum kita menggunakan komputer untuk menyelesaikan sesuatu masalah, kita harus mengarahkan komputer tersebut untuk mengikut prosedur tertentu dan menyelasaikan tugas yang dikehendaki

Ianya melibatkan beberapa langkah:
1) Menukarkan masalah tersebut ke dalam beberapa langkah set logik yang komputer boleh diikut
2) Memberitahu komputer supaya mengikut dan melengkapkan set logik tersebut.


1.1 Computer algorithm.
Set logik yang lengkap untuk menyelesaikan masalah komputer tertentu dipanggangil "computer/numerical algorithm.

contoh:



1.2 Computer language (Bahasa komputer)

Program komputer yang membolehkan manusia berkomunikasi dengan komputer.
komputer program atau kod adalah pengumpulan kenyataan yang  biasanya akan ditulis dalam bahasa program komputer.


1.3. Kod komputer
Bits dan bytes.

Komputer hanya menggunakan sistem nombor binari sebagai nombor asas untuk beroperaso.

Dalam sistem binari, hanya ada 2 simbol sahaja. Iaitu "0" dan "1" sahaja.
Contoh: 110010011

setiap nombor binari tersebut dirujuk sebagai bit.

8 bit = 1 byte
4 bit = 1 nibble


1.4. Bahasa program komputer.
Terdapat 2 jenis:

a. bahasa tahap rendah
bahasa tahap rendah adalah bahasa primitf ataupu kod binary seperti "1110011"

b. bahasa tahap tinggi.
Komputer digunakan untuk menukarkan bahasa tahap tinggi kepada kod.



Contoh:

// operating with variables

#include <iostream>
using namespace std;

int main ()
{
  // declaring variables:
  int a, b;
  int result;

  // process:
  a = 5;
  b = 2;
  a = a + 1;
  result = a - b;

  // print out the result:
  cout << result;

  // terminate the program:
  return 0;
}

Observable, Operator and Expectation Value

The wavefuntion in part 1 cannot be measured directly, but it average intensity is equivalent to the relative probability of finding the particle in position x, at time t.


Wavefuntion di bahagian 1 tidak boleh di kira secara terus, tetapi purata keamatannya bersamaan dengan kebarangkalian untuk mencari zarah di kedudukan x, pada masa t.

This is consequence of uncertainty principle where position, momentum and energy of the particle cannot in general be precisely determined.


Ini adalah kerana dari prinsip ketidakpastian (uncertainty principle) menyatakan bahawa, kedudukan, momentum dan tenaga tidak boleh ditentukan secara tepat.


The average value of these quantity are called expectation value.


Nilai purata untuk kuantiti ini dipanggil nilai jangkaan (expectation value).

Expectation value <Â> with respect to the state Ψ(r,t) is define by 


Nilai jangkaan <Â> yang berkait dengan keadaan Ψ(r, t) ditakrifkan sebagai

to related QM observable position (x), momentum (p), and energy (E),  the expectation value of the measurable parameter is the calculated expectation value.


untuk mengkaitkan Kuantum Mekanik kedudukan (x), momentum (p), dan tenaga (E), nilai jangkaan yg boleh diukur parameter diukur ialah nilai jangkaan yang dikira.

the energy of the system is given by the expectation value of the Hamilton. 

tenaga dalam sistem tersebut di nyatakan dalam nilai jangkaan Hamilton.

nampak macam pening..tapi tenang.. cuma tambah wavefuntion dan conjugate wavefuntion.. Ianya bertujuan untuk mengira keamatan (intensity) nilai tersebut kerana, ianya tidak boleh dikira secara terus ke posisi, momentum, atau tenaga secara terus.