Observable, Operator and Expectation Value

The wavefuntion in part 1 cannot be measured directly, but it average intensity is equivalent to the relative probability of finding the particle in position x, at time t.


Wavefuntion di bahagian 1 tidak boleh di kira secara terus, tetapi purata keamatannya bersamaan dengan kebarangkalian untuk mencari zarah di kedudukan x, pada masa t.

This is consequence of uncertainty principle where position, momentum and energy of the particle cannot in general be precisely determined.


Ini adalah kerana dari prinsip ketidakpastian (uncertainty principle) menyatakan bahawa, kedudukan, momentum dan tenaga tidak boleh ditentukan secara tepat.


The average value of these quantity are called expectation value.


Nilai purata untuk kuantiti ini dipanggil nilai jangkaan (expectation value).

Expectation value <Â> with respect to the state Ψ(r,t) is define by 


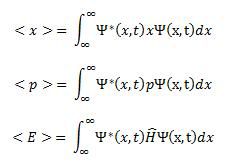
Nilai jangkaan <Â> yang berkait dengan keadaan Ψ(r, t) ditakrifkan sebagai

to related QM observable position (x), momentum (p), and energy (E),  the expectation value of the measurable parameter is the calculated expectation value.


untuk mengkaitkan Kuantum Mekanik kedudukan (x), momentum (p), dan tenaga (E), nilai jangkaan yg boleh diukur parameter diukur ialah nilai jangkaan yang dikira.

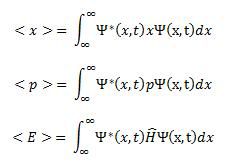
the energy of the system is given by the expectation value of the Hamilton. 

tenaga dalam sistem tersebut di nyatakan dalam nilai jangkaan Hamilton.

nampak macam pening..tapi tenang.. cuma tambah wavefuntion dan conjugate wavefuntion.. Ianya bertujuan untuk mengira keamatan (intensity) nilai tersebut kerana, ianya tidak boleh dikira secara terus ke posisi, momentum, atau tenaga secara terus.